Part 2 : Following along MIT intro to deep learning
Abhijit Ramesh / March 14, 2021
13 min read • ––– views
Deep Sequence Modeling
Introduction
Given the position of a ball can we predict where the ball is going next ?, Yes we can, but it would only be a random guess. But instead of just the position of the ball if we are given its previous positions in each times step can we predict the next position, Yes we can. This kind of predictions is called sequential modelling.
Sequence Modeling
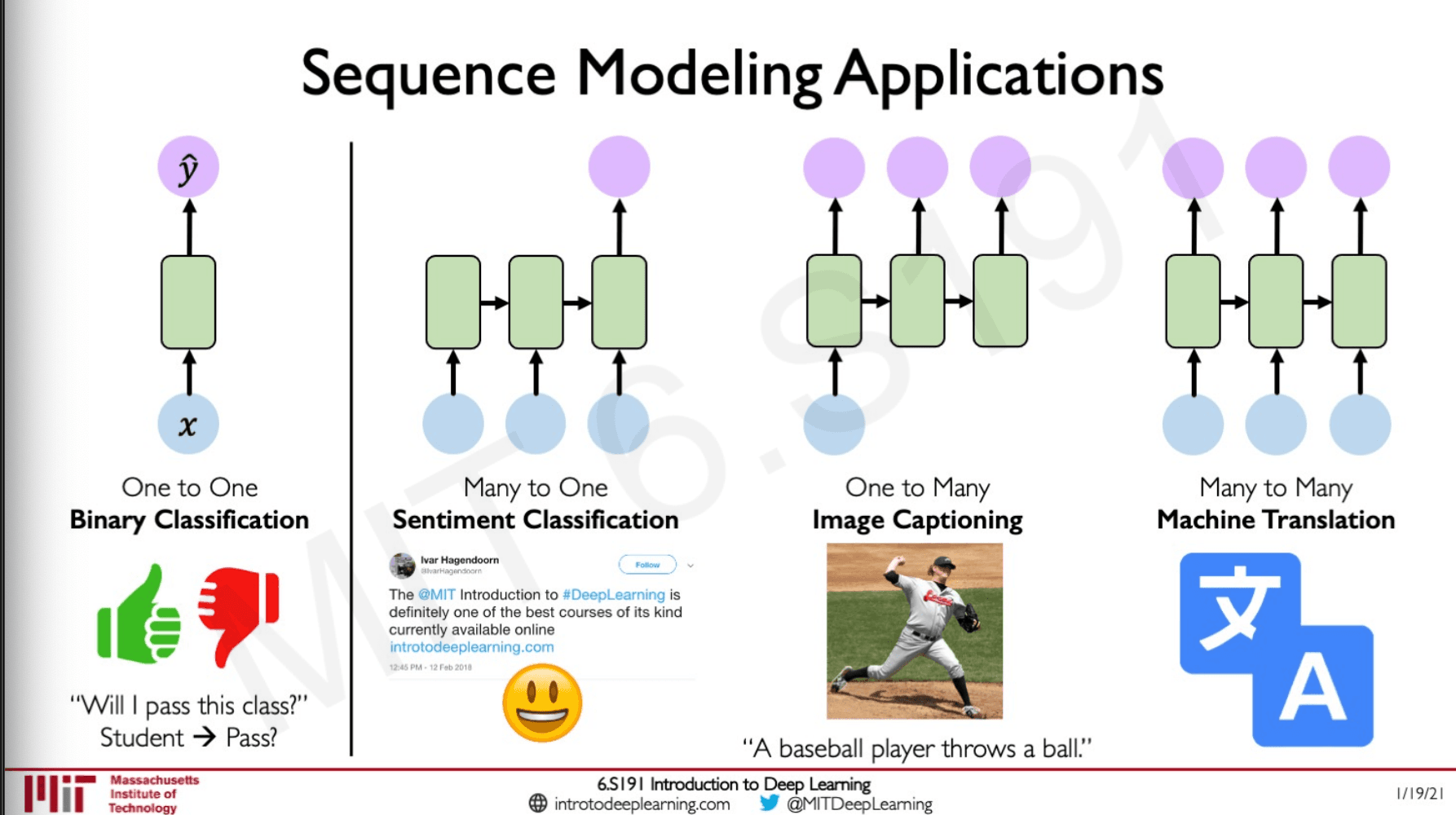
Previously we looked at binary classification where when we are given an input we should predict whether we would pass the particular class or not. Now we are going to look at models that will deal with sequences of data.
Many to One
These are like sentiment classification where we have a sequence of characters or words, and we have to figure out if the model statement is positive or negative.
One to Many
These are application where we give an input for example an image, and the output would be a sequence of characters or words like some description of the image.
Many to Many
These are application where we have a sequence of inputs, and our intention is to generate a sequence of outputs.
Neurons with recurrence
Let's get the idea of what recurrence is with the help of a perceptron.
In a preceptor, we generally have one or more inputs, and a hidden layer leading to one or more outputs. The preceptor does not have any notion of time but let's think of it this way.
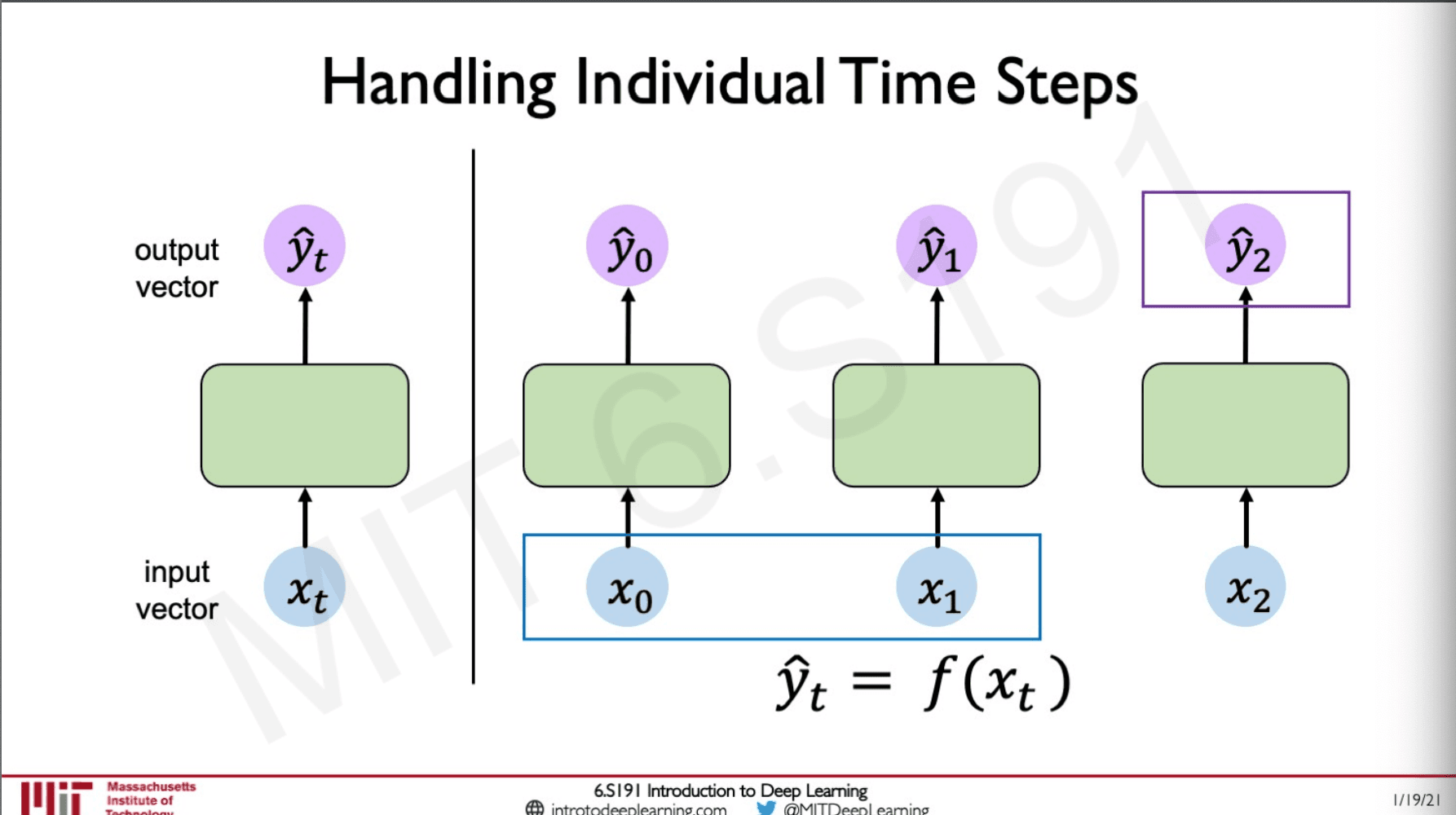
Here we are using the same perceptron again and again and passing in the sequence which is time-dependent one by one into the same perception to generate an output. When we think about it the output lets say y_hat 2 must be related to x1 and x0 since there are some temporal dependencies.
In order to save this, we use something called a cell state, and we pass these cell states from one network to the other even though they are the same preceptor.
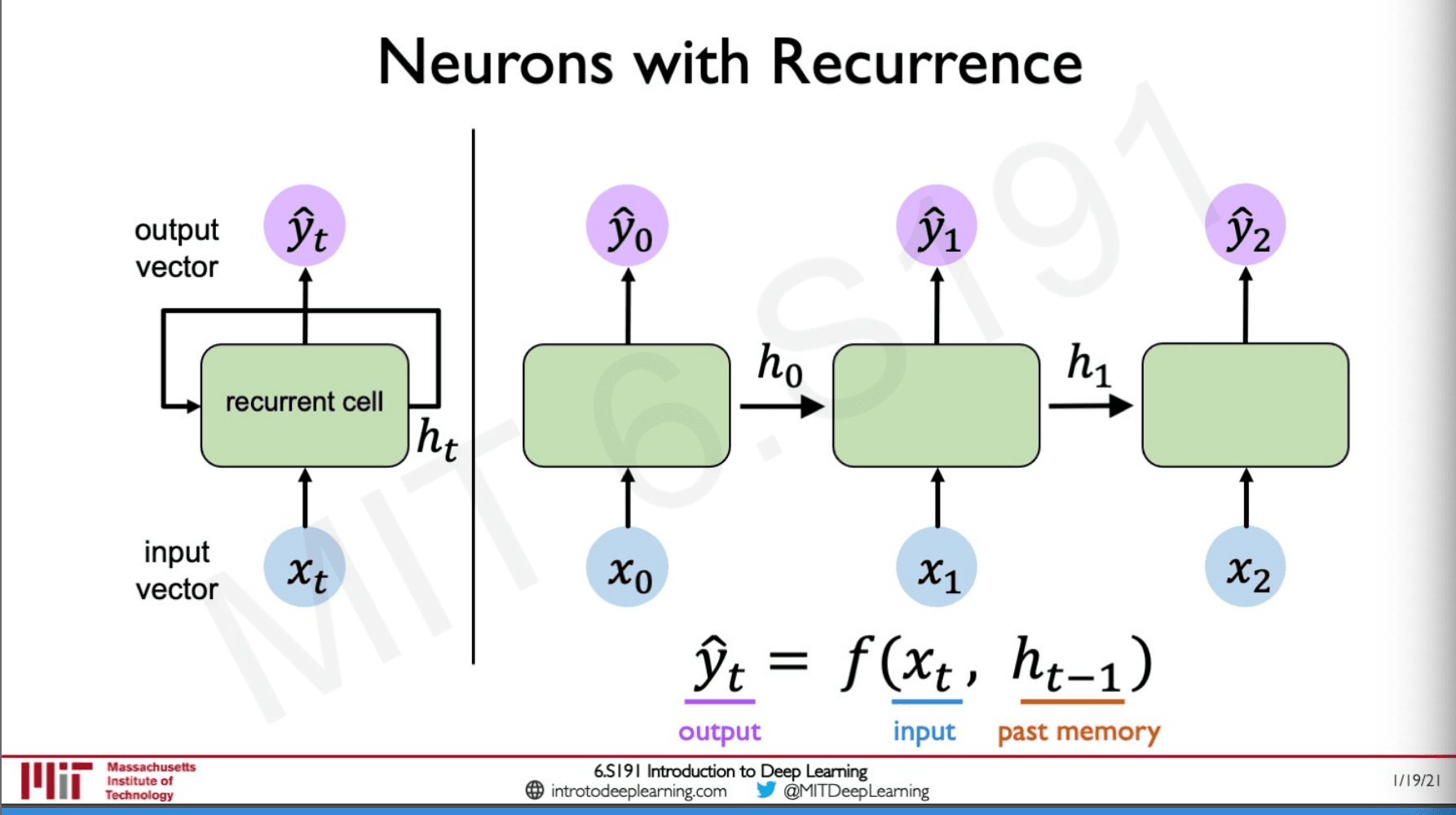
This sort of establishes a recurrence (the loop) in the same perceptron and hence these networks are called a recurrent neural network.
Recurrent Neural Networks (RNNs)
The most important aspect of recurrent neural network is the state, , which gets updated in every time step as the sequence is being passed through the network.What does it mean by passing a sequence though a network ?
We apply the recurrence relation,
Here,
- is the cell state
- is the function with weights W
- is the input
- is the old state
my_rnn = RNN()
hidden_state = [0,0,0,0]
sentence = ["I","love","recurrent","neural"]
for word in sentence:
prediction, hidden_state = my_rnn(word,hidden_state)
next_word_prediction = prediction
This is what a pseudo code for an RNN would look like the first 3 lines are just basic initialisation of the network.
The Loop after that loops through the sentence each time making a prediction as well as an update to the hidden state.
Initially the hidden state given is just an array of 0's this array along with the word is given to the rnn where it will return the prediction, and the update on the hidden state.
finally, we can see the new word by just checking what value is held in the prediction variable.
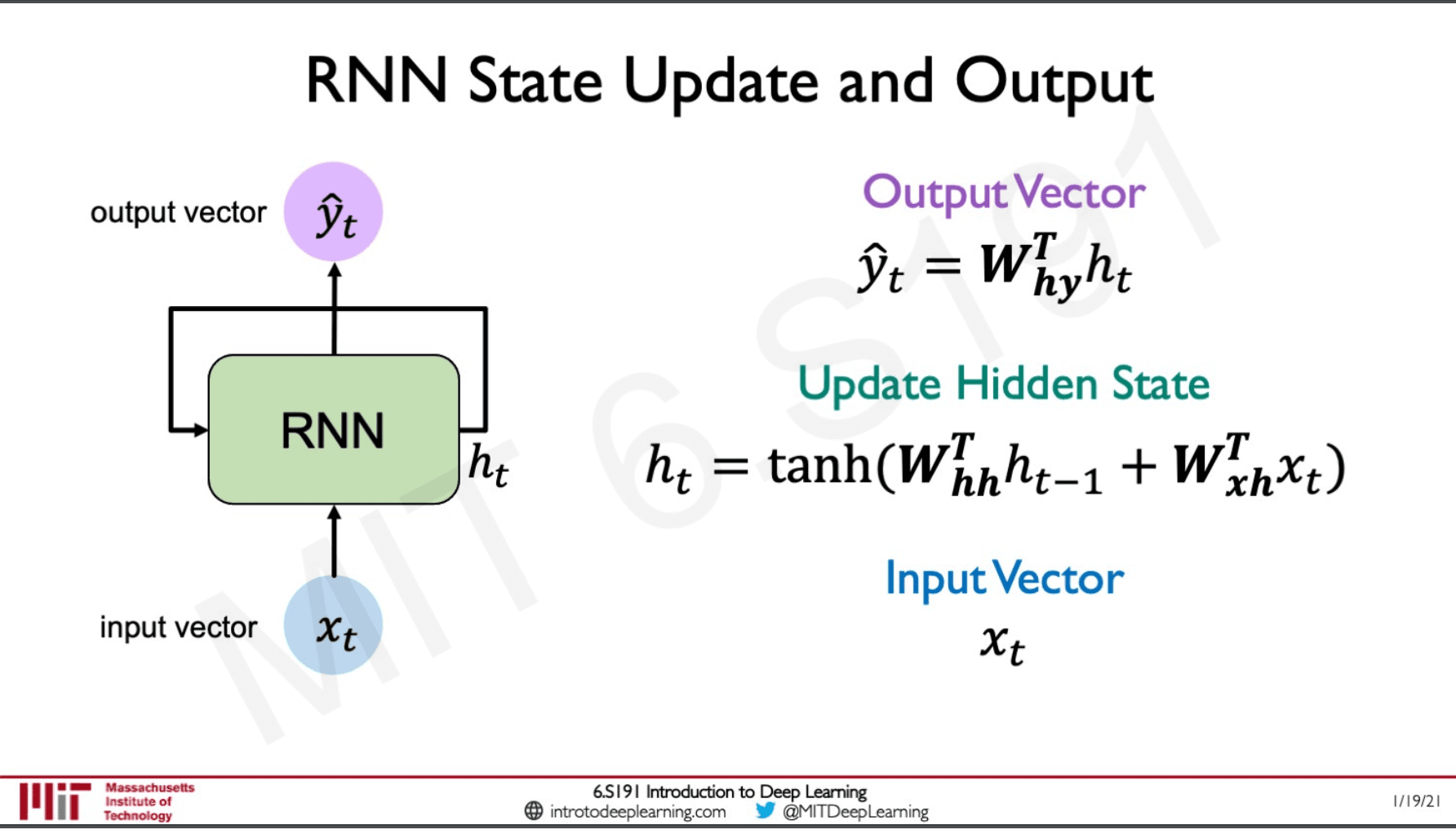 Let's see how this happens mathematically, we have the input the hidden state and finally our output . We have weights for each of these components the weights for the hidden layer, the weights for the input and finally the weights for the output.
Let's see how this happens mathematically, we have the input the hidden state and finally our output . We have weights for each of these components the weights for the hidden layer, the weights for the input and finally the weights for the output.
The update on the hidden state is done by multiplying the weight of the input state to the hidden state of that time-step and multiplying the weight of the input with the input. This is then passed through a non-linear activation function in our case a hyperbolic tangent.
Before being given as an output the hidden state vector is multiplied with the weights of the output layer.
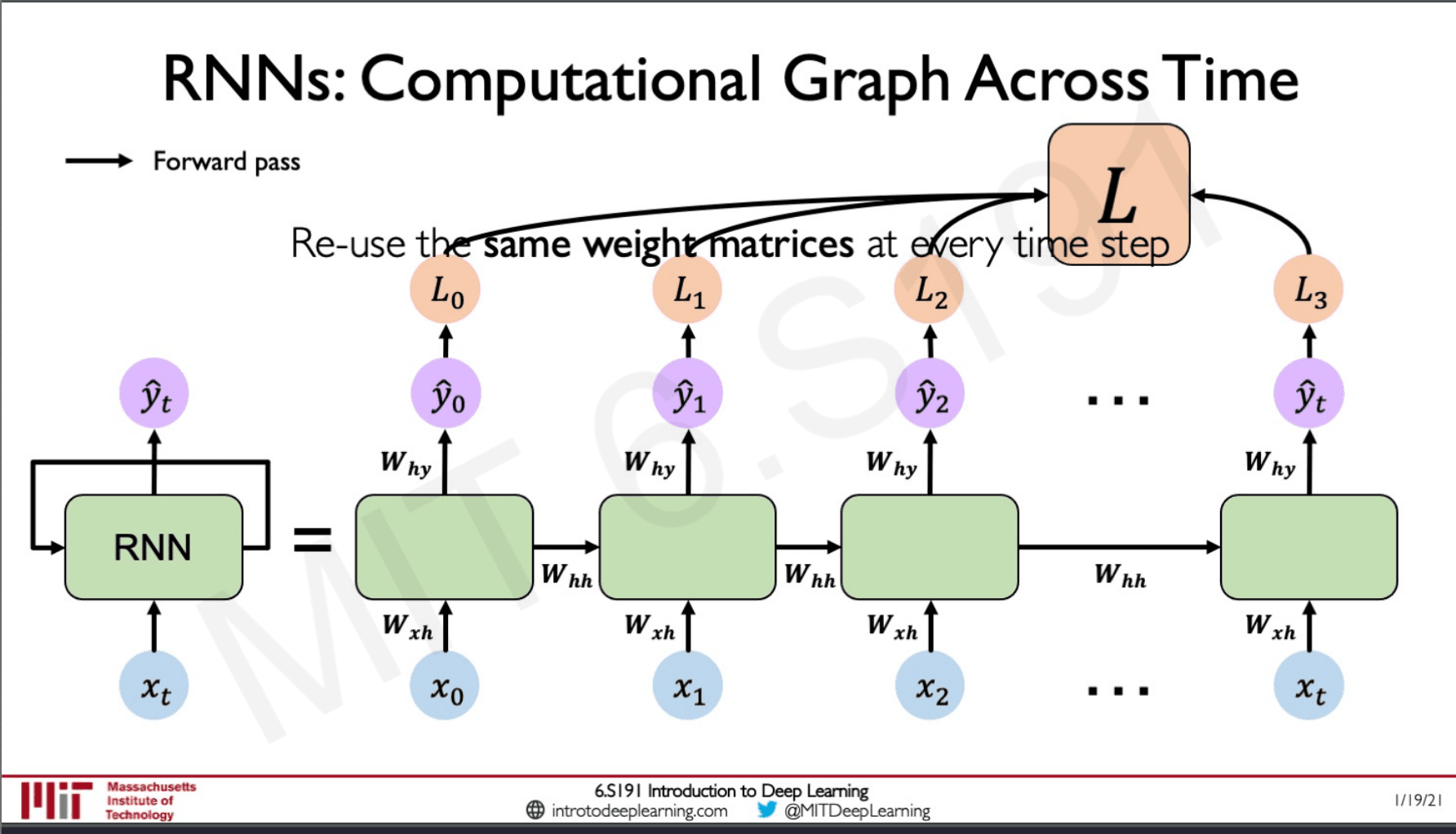
To get a better understanding the feedback loop on the RNN is always unfolded and represented as the slide above this will help us visualise how the RNN behaves in each time-step. The weights of the RNN are reused in each time step and for every input apart from the hidden state / cell state being updated there is an output that is generated as well. These outputs are used to computer the loss of the network in that time step and we can finally sum all these losses to find what the total loss of the network is.
From which we can train this network.
RNNs from Scratch
class MyRNNCell(tf.kreas.layers.Layers):
def __init__(self,rnn_units,input_dim,output_dim):
super(MyRNNCell,self).__init__()
self.W_xh = self.add_weights([rnn_units,input_dim])
self.W_hh = self.add_weights([rnn_units,rnn_units])
self.W_hy = self.add_weights([output_dim,rnn_units])
self.h = tf.zeros([rnn_units,1])
def call(self,x):
self.h = tf.math.tanh(self.W_hh * self.h * self.W_xh * x)
output = self.W_hy * self.h
return output, self.h
We are extending the layer class so that we can use the RNNCell we create as layers in any neural network.
class MyRNNCell(tf.kreas.layers.Layers):
def __init__(self,rnn_units,input_dim,output_dim):
super(MyRNNCell,self).__init__()
self.W_xh = self.add_weights([rnn_units,input_dim])
self.W_hh = self.add_weights([rnn_units,rnn_units])
self.W_hy = self.add_weights([output_dim,rnn_units])
self.h = tf.zeros([rnn_units,1])
The weights have been initialised by this code snippet and we are also initialising the hidden layer to be 0's as said earlier.
Then we define our forward pass,
def call(self,x):
self.h = tf.math.tanh(self.W_hh * self.h * self.W_xh * x)
output = self.W_hy * self.h
return output, self.h
This is very self-explanatory to us now that we have seen the mathematical and diagrammatic visualisation of how the RNN works.
We actually don't to write code in tensor-flow to make our RNN we can simply use this
tf.keras.layers.SimpleRNN(rnn_units)
Design Criteria
- Handle variable-length data
- Track long-term dependencies
- Maintain information about order
- Share parameters across the sequence
A Sequence modeling problem
Predict the next word
Let us say that we have a sentence "This morning I took my cat for a walk" the idea is that when the network is given the sequence "This morning I took my cat for a" it should predict "walk". The problem here is that neural networks uses mathematical functions achieve some task and we are not doing that we have characters and we need to find some way convert these characters to numbers.
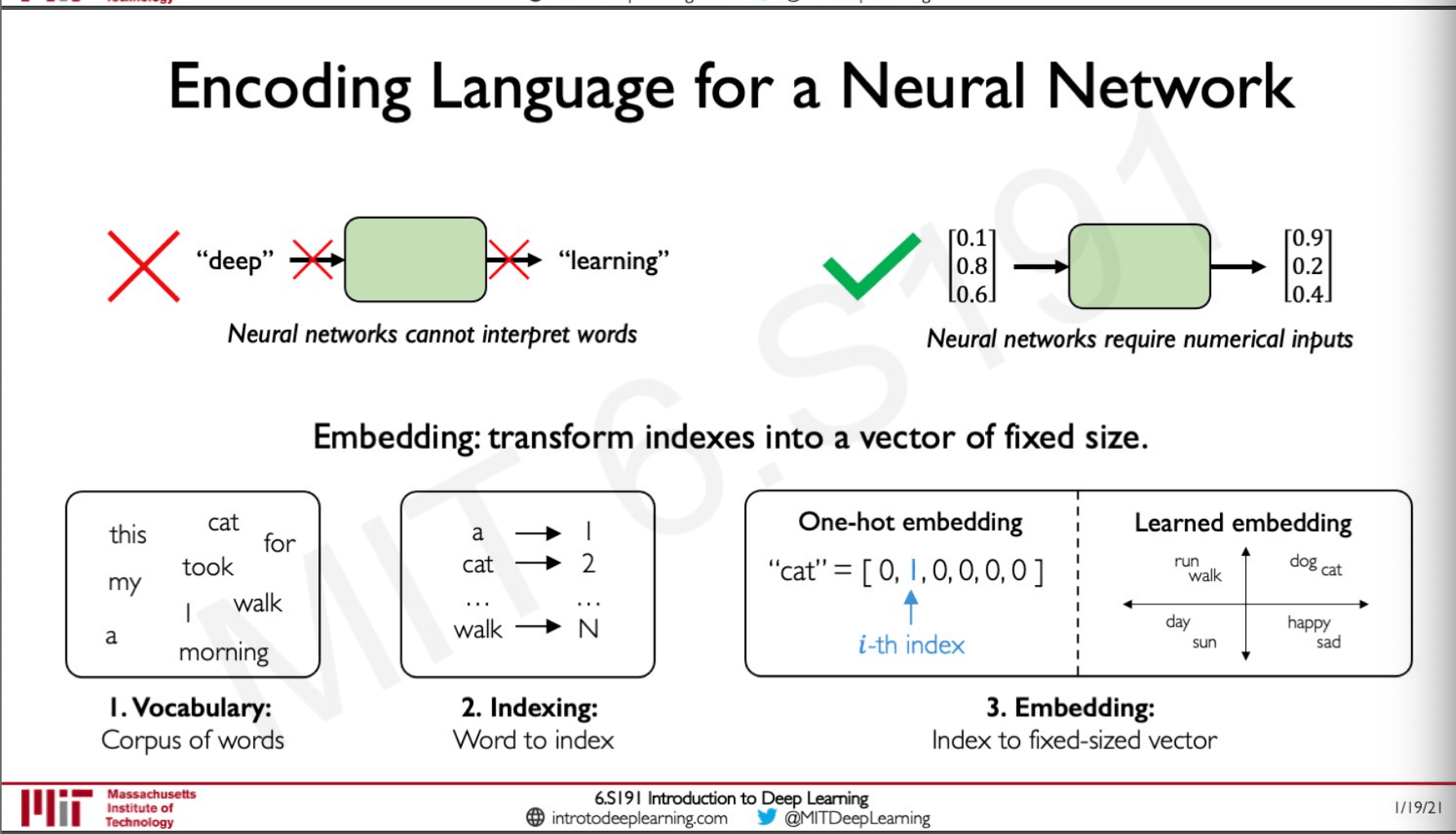
This is where encoding comes to play,
First we collect our vocabulary which is the corpus of words, then we need to index these words by mapping them to a number. Once this is done we can do either of the two methods to do embedding, one is take a sparse binary vector which has the length equal to our vocabulary of words and has a 0's and 1 where the 1 will indicate the presence of a word. Another method to follow is to actually learn these vocabulary by passing the index mapping to the model and the model will transform this index mapping to all the words in our vocabulary to a vector of a lower dimensionality such that the values of these vectors are learned so words with similar meaning would have similar embeddings.
RNNs meet all our design criteria, we can have sentences of different length since each word in the sequence is going to be treated as the input in a timestep.
Handle Variable Sequence Length ✅
Since the inputs are fed sequentially, and we have a hidden cell state to remember what is has learned from the past the network uses the information in the distinct past to make a prediction.
Model Long-Term Dependencies ✅
RNNs are able to differentiate between something like "The food was good, not bad at all." and "The food was bad, not good at all". Even though the vocabulary is the same the order matters since the input is temporal.
Capture differences in sequence order ✅
The hidden cell state, and the weights of the network are all shared parameters in the network across all the timesteps.
Share parameters across the sequence ✅
Backpropagation Through Time
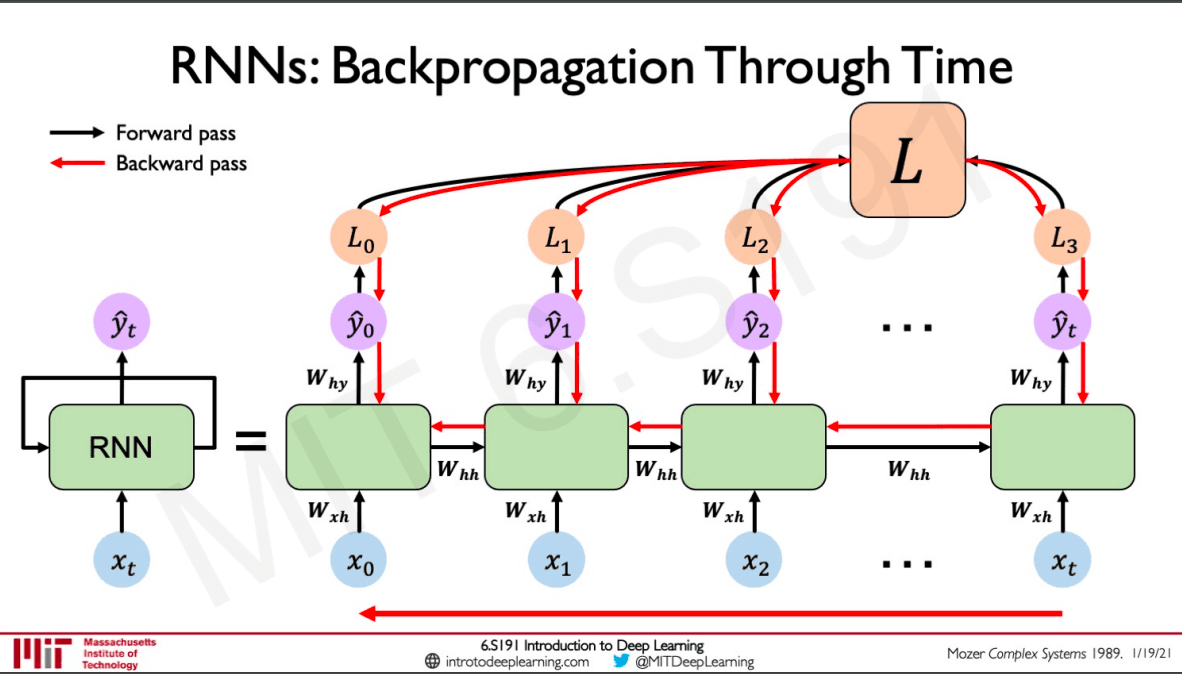
Compared to a feed-forward network where we would back-propagate through the network by taking derivatives of the loss with respect to each parameter, and then we adjust the parameters to minimise the loss. For RNNs the forward propagation takes place in time steps by passing the hidden state from one time step to another and in each time step also creating an output from which we can derive a loss for that particular time step, summing all these losses would give us the total loss. Instead of backpropagating through a single feed-forward network here, we have to backpropagate through the overall loss to the networks as well as across the network from what time step we are right now to the past time steps to the beginning and hence backpropagation through time.
Drawbacks
The standard RNN have some drawbacks when we think about the operations being done on the weight matrices. We can see that for the calculation of a gradient with respect to many factors of is being used and there is the repeated computation of this which could lead to two extreme problems.- Exploding gradients this happens when many values are greater than 1 the gradients go beyond control, and we are not able to get good results we can counter this by using gradient clipping to scale the bigger gradients.
- The other extreme is when many values are smaller than 0 this would lead to vanishing gradient.
What are vanishing gradients ?
This happens when we multiple small numbers together, imagine multiplying values between 0 and 1 together this would create a small number and what if this happens for many iterations the gradient becomes almost nothing. What this means can be explained with an example.
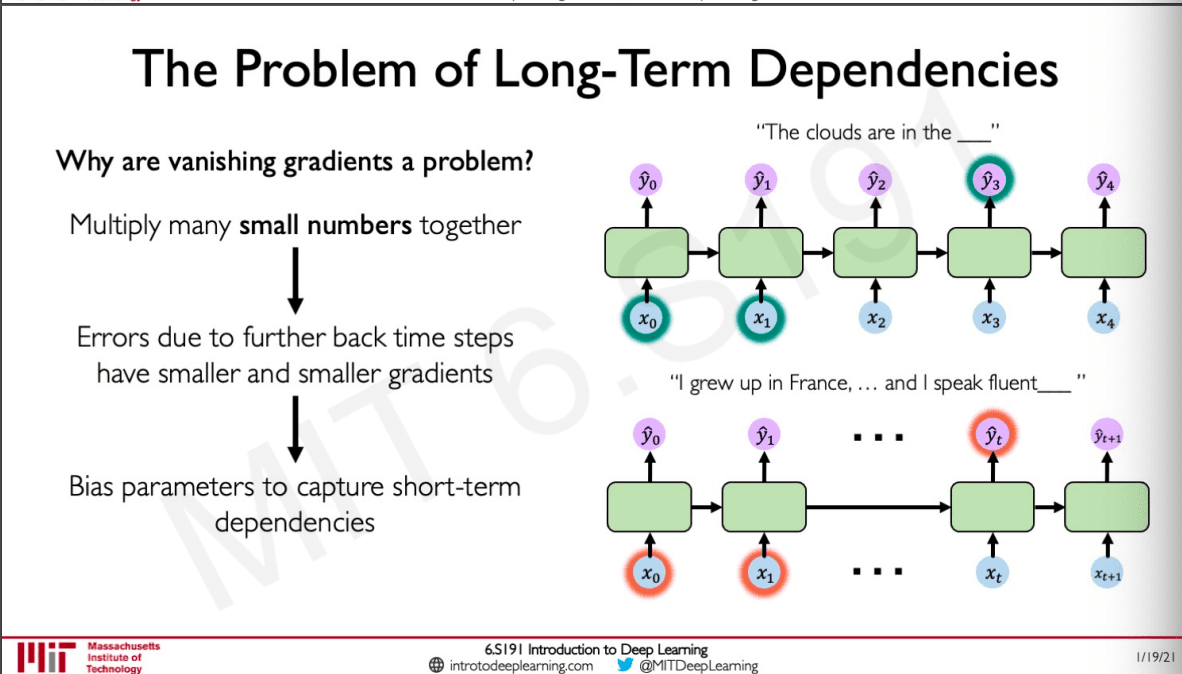
If we have a sentence like "The clouds are in the ____" the network is able to predict the answer because relevant information is in a very close timestep. But the problem happens when there is a long term dependency as in the case of "I grew up in France,....... and I speak fluently ____"
In this case the relevant information is far behind in the time step which would be used to predict the next word.
There are some ways to solve this,
Activation Functions
We can select a smart activation function such as ReLU which would prevent the derivative of the function from shrinking the gradient when the value is less than 0.
Parameter Initialization
We can initialise the weights to be an identity matrix, and biases to zero this will prevent shrinkage to zero,
Gated Cells
These are advanced RNNs which implement something called as gates which control the information that is passed through. This will track the information through many time steps and use this information according to what the architecture design is deciding how this information should flow.
One of the most common and state of the art of such cells are LSTMs.
Long Short Term Memory (LSTM) Networks
A standard RNN have the following features
- a which is coming from the previous state
- An input
- After being multiplied with their respective weights they are passed through a tanh activation
- An output
- A hidden layer update
But an LSTM looks something like this,
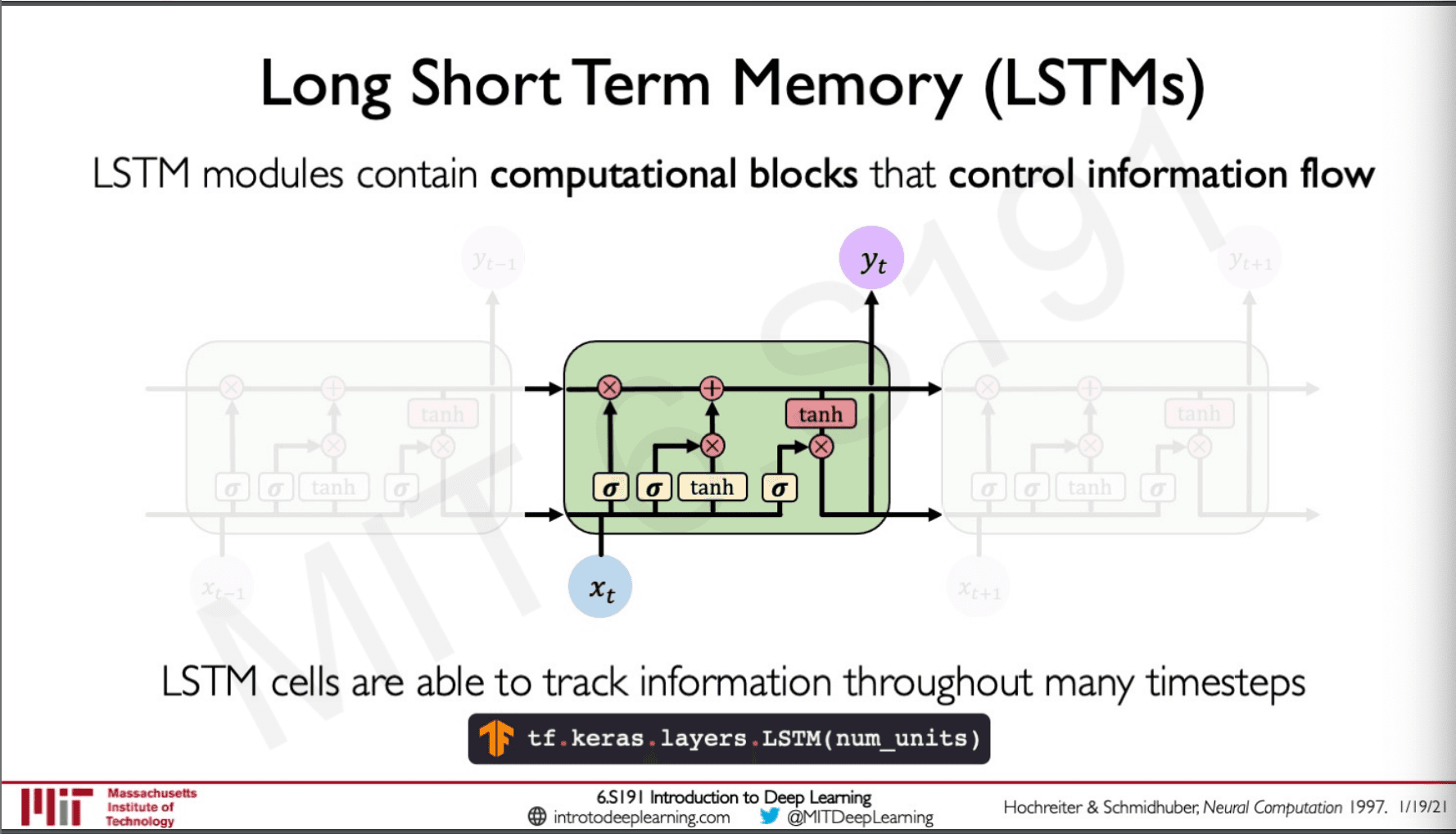 They also have standard neural network activations and operations what I mean by this is that the indicates a sigmoid activation function and the x, + indicates pointwise multiplication and addition respectively.
They also have standard neural network activations and operations what I mean by this is that the indicates a sigmoid activation function and the x, + indicates pointwise multiplication and addition respectively.
These are gates which allows the LSTM to do four functions,
- Forget
- Store
- Update
- Output
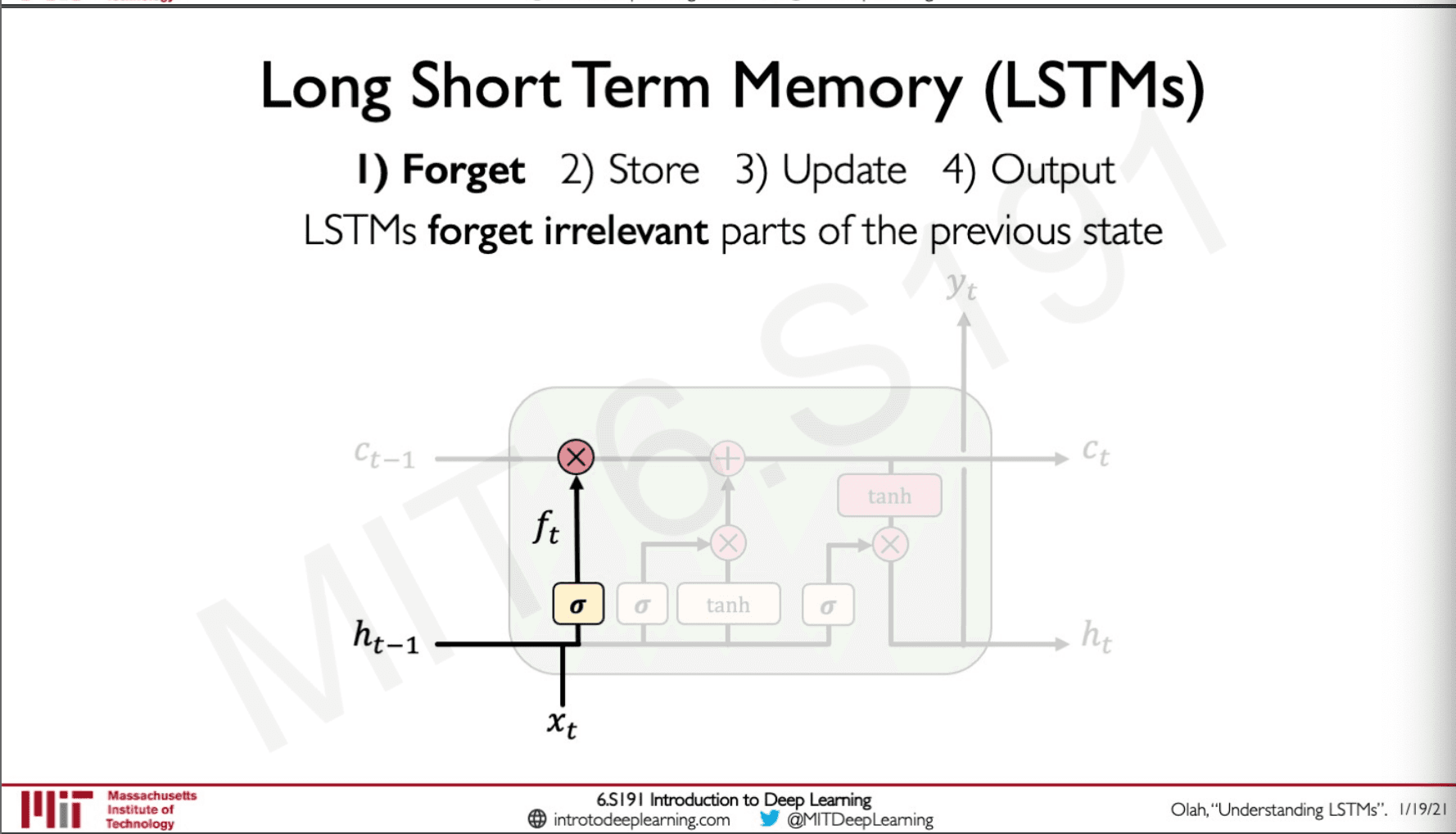
The input and the hidden state is first gated and passed through a point multiplication cell this is done to forget the irrelevant information.
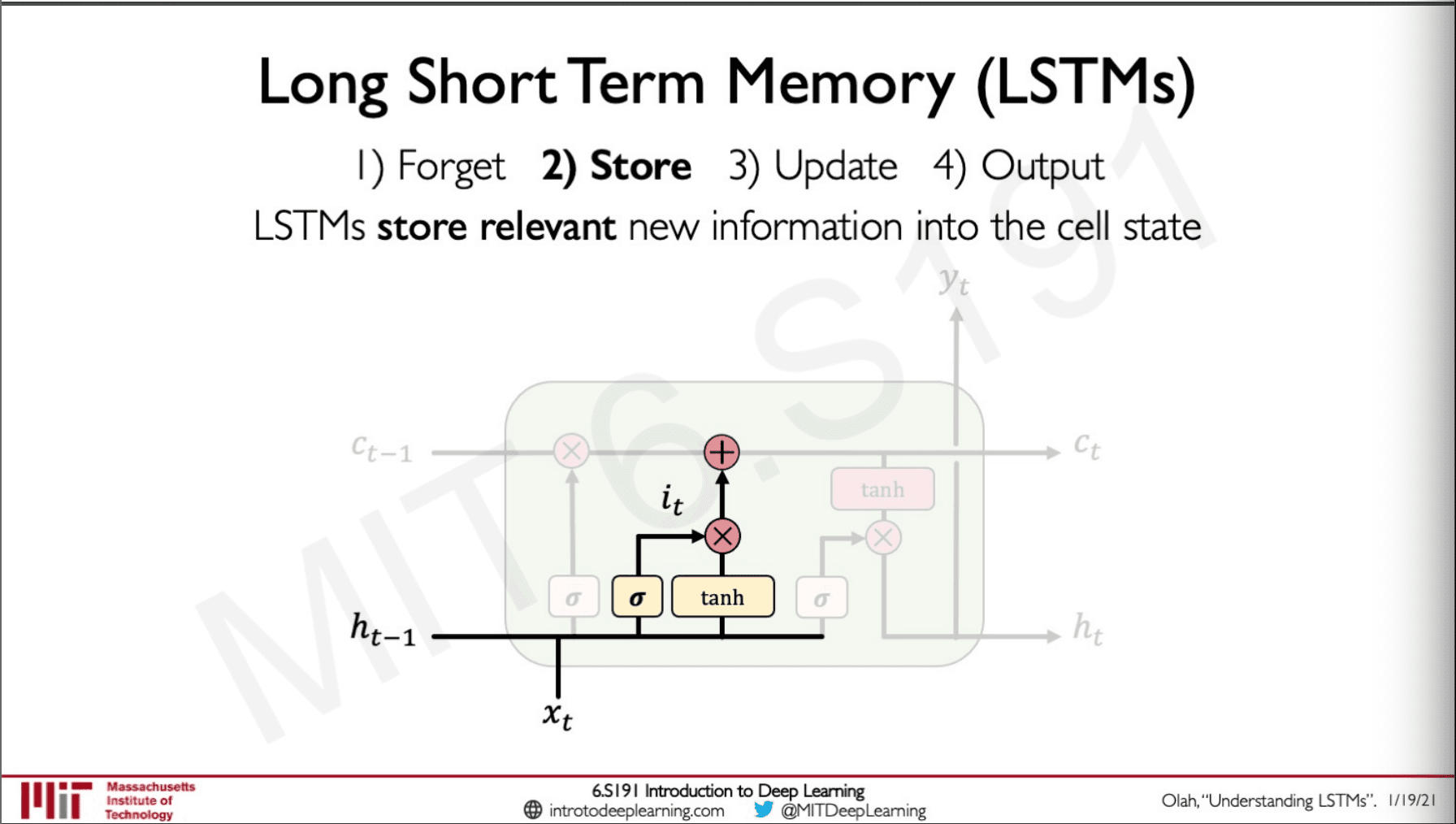
Next is the update state which take in the hidden state and input and determines which are relevant information to be kept in the network.
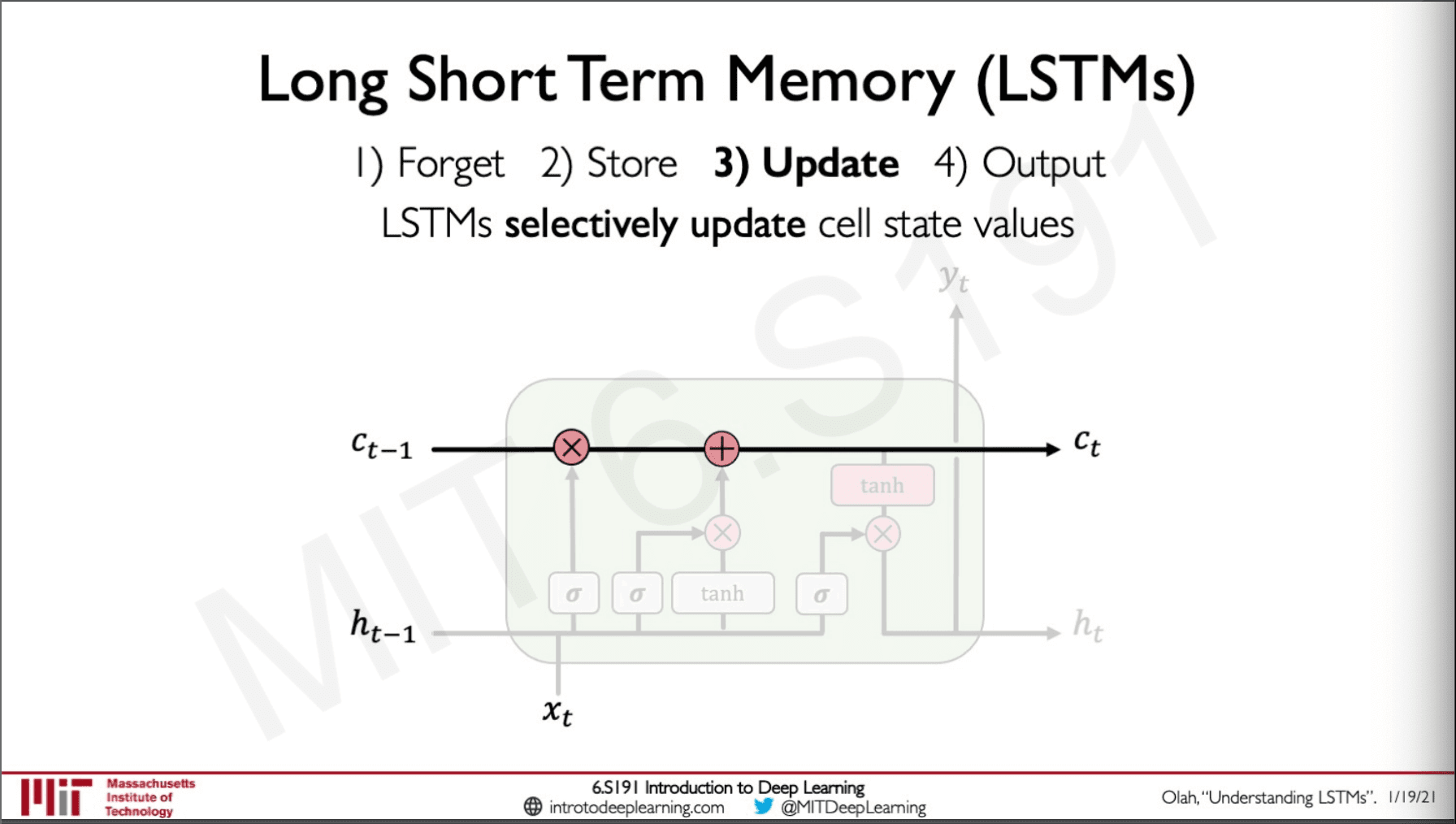 From the output of the forget and store state, the LSTM selects what values are to be updated, and a new cell state is used to pass this to the next time step. This is an extra addition compared to the RNN in the states.
From the output of the forget and store state, the LSTM selects what values are to be updated, and a new cell state is used to pass this to the next time step. This is an extra addition compared to the RNN in the states.
Finally we have the output state which controls the information to the next time step.
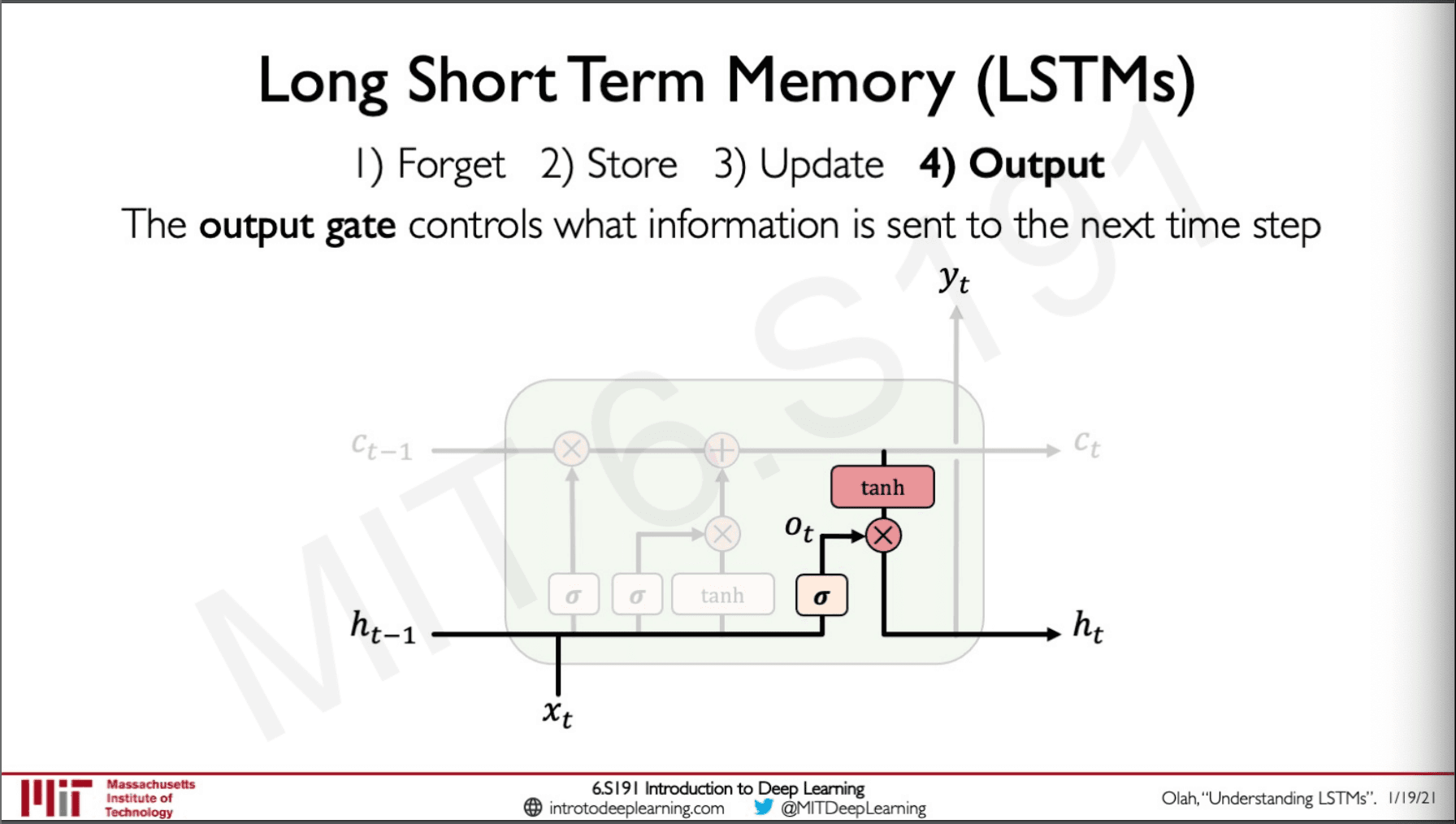
TL;DR LSTMs
They have mechanism which controls what information should be passed to the next state.
The back-propagation through time will give us the benefit of having uninterrupted gradient flow.
RNN Applications
Music Generation
Music similar to characters in a sentence are also sequential data so if we feed the music sheet to an RNN and ask it to predict what the next character it is would be trained for the task of music generations and can be used there after.
Sentiment Classification
Given an sequence of characters like a tweet we are able to predict if the output is a positive or negative sentiment.
Machine Translation
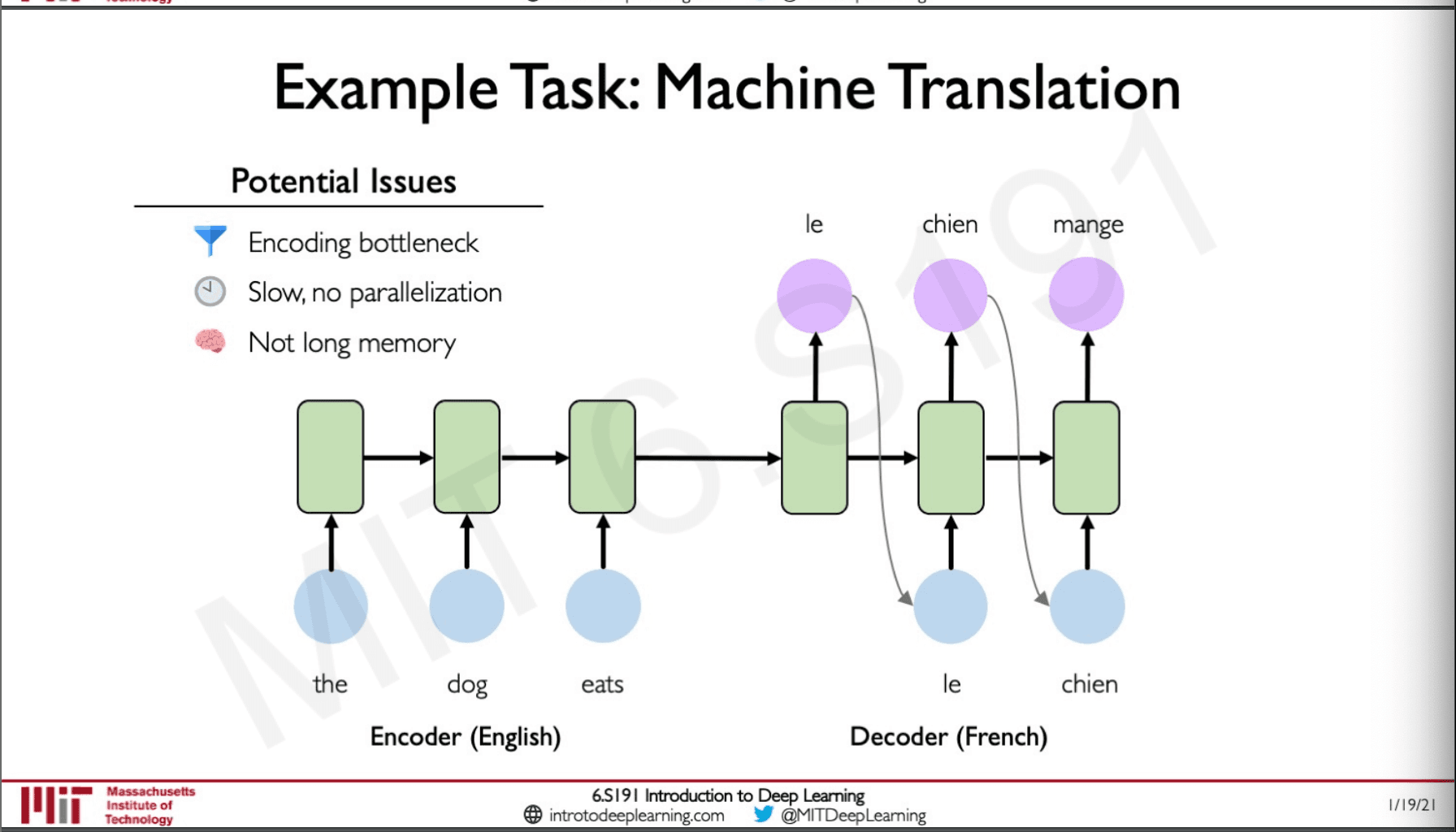
RNNs can be used for machine translation which is translating one language to another this is done by Encoder Decoder architect where the data in one language is encoded and is passed as a state vector to another decoder where it will generate the translations.
There are some drawback to this, the Encoder is bottleneck as the state vector which is passed to the decoder is a compressed version of the vectors that are learned in the encoder and this would lead to some data being lost when we move to the decoder.
All this process happens sequentially hence it cannot be parallelized.
Traditional RNNs do not have a very good long memory because of the vanishing gradient problem.
Back-propagation is very expensive It has to move back in time the number of time steps it passed in forward-propagation to do one step of backpropagation.
Attention
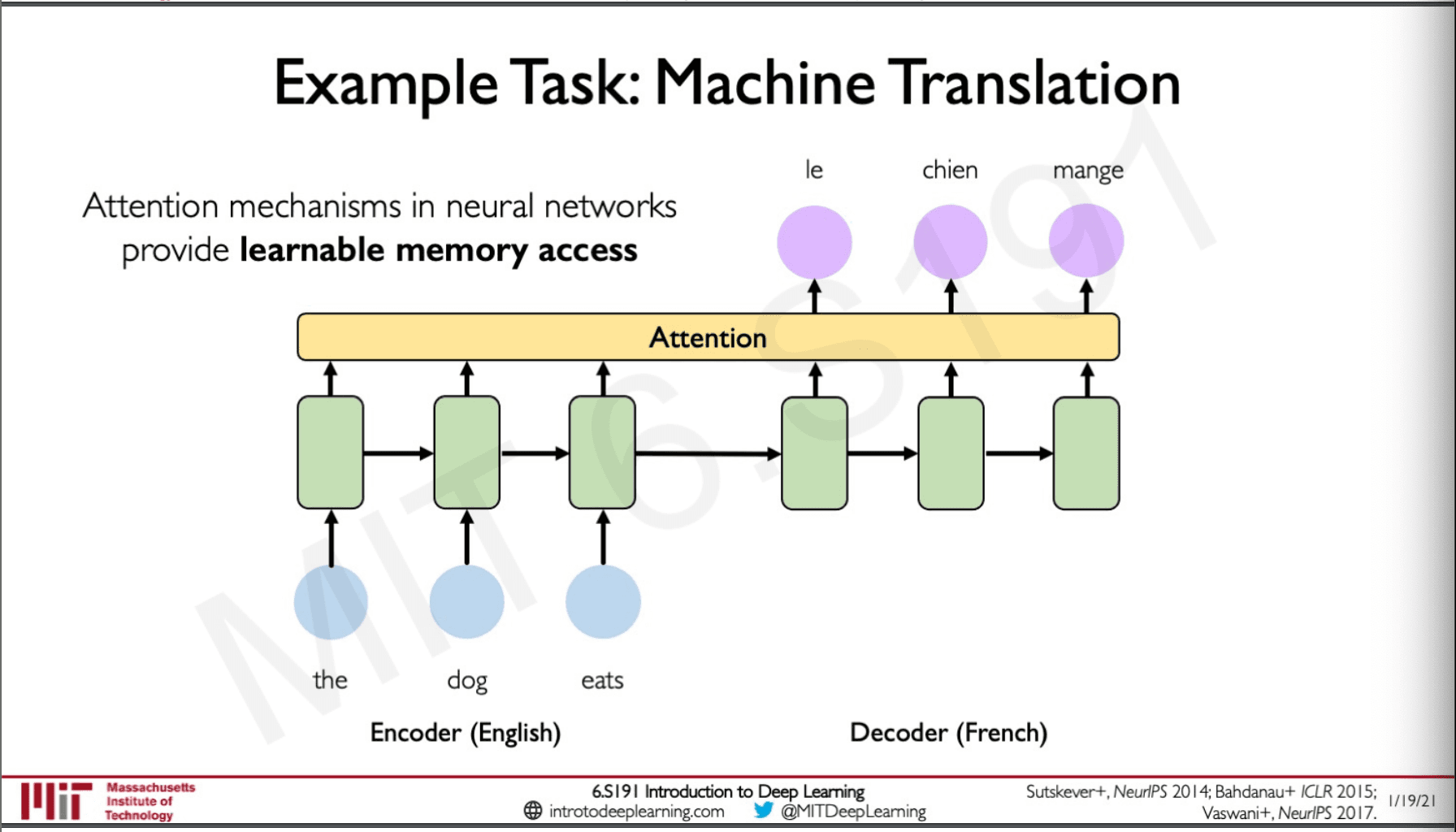
Attention introduces an intermediate layer which can give the future time step not only access to the state vector which is passed to them but also to each of the state in the encoder this allows the decoder to get access to more information. This points to which state to attend to and hence making the network more capable to capture long term dependencies. The benefit of this is that it only requires one single pass and no backpropagation through time is required.
Attention is used in many celebrated applications of deep learning like self-driving cars and environment modeling.
Sources
MIT intro deep learning : http://introtodeeplearning.com/
Slides on intro to deep learning by MIT : http://introtodeeplearning.com/slides/6S191_MIT_DeepLearning_L2.pdf
Lab Solutions
https://github.com/abhijitramesh/learning-introtodeeplearning/blob/main/Part2_Music_Generation.ipynb
Subscribe to the newsletter
Get emails from me about machine learning, tech, statups and more.
- subscribers